
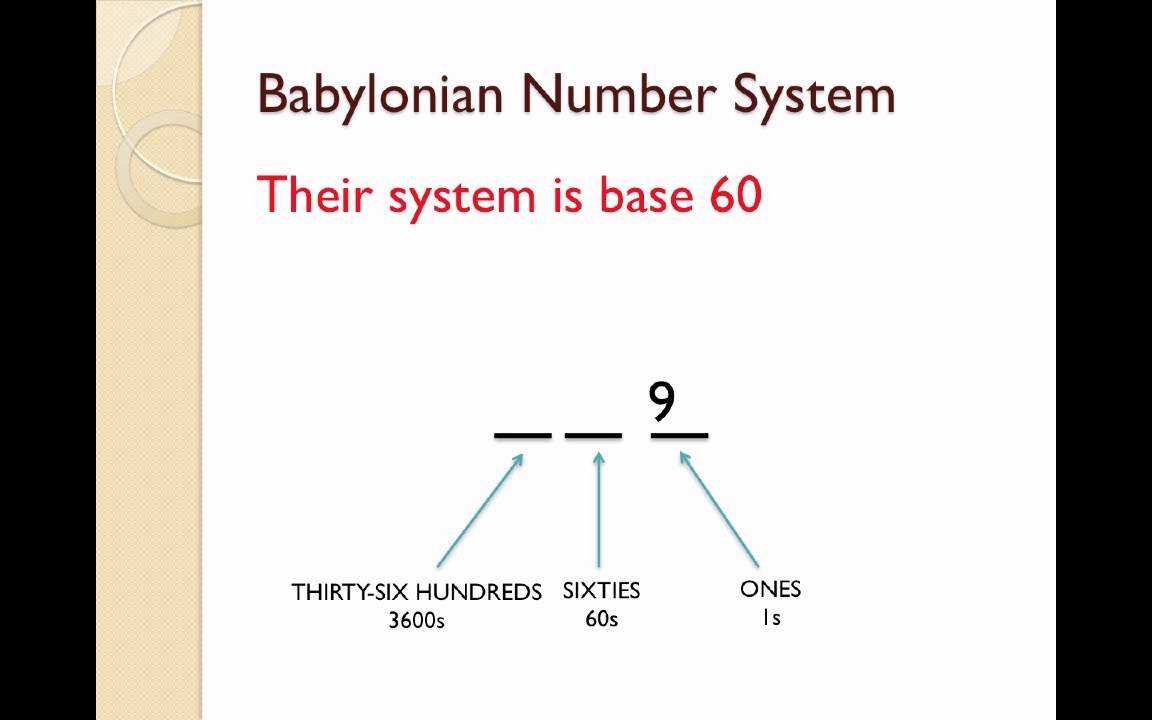
If we exceed the available values in a place, we go to the leftĪ base 2 system is the basis for computer representations of numbers.First rule of base X, don’t talk about X.) (Remember, X is not a symbol, it is a combination of 1 and 0.There are only X symbols (0 through X-1).Every place is worth X times the place on its right.If we exceed the available values, we go to the left.(Remember, 10 is not a symbol, it is a combination of 1 and 0.).There are only ten symbols (0 through 9).Every place is worth 10 times the place on its right.Place to the left of the decimal is worth 1.These bases provide different representations of the same number.We can use any number as the basis of a place-value system.

Notice that although we don’t always write the decimal point, its position is always important. The value of a digit depends on its position relative to our decimal point. Modern Numbers Base 10 Place Value Systems The invention of the zero was a significant advance in our number systems. Early number systemsĮarly number systems seem reminiscent of a tally system. Why can we represent any number between positive and negative infinity with only ten distinct symbols? The answer is that the position of each symbol relative to the other numbers changes its value.Īnother question for you to think about is, why do you “carry the one” when you add and multiply? Morpheus knows why you carry the one. This section explores our number system and how it works.


 0 kommentar(er)
0 kommentar(er)
